图：北京航空航天大学经管学院金融系教授、博导，李平

编者按：

在2017中国资产证券化论坛年会上，北京航空航天大学经管学院金融系教授、博导，李平介绍了关联模型的基本原理以及如何应用于结构化金融产品定价，并结合案例分析了国内外相关产品的定价思路。

 

李平（北京航空航天大学经管学院金融系教授、博导）：

 

首先非常感谢会议主办方邀请我过来做这样一个讲座，这是一个资产证券化的会议，我近十年来一直在研究关联模型在金融中的应用，所以庞阳老师就邀请我过来了。今天我想给大家介绍一下如何用关联模型做结构化金融产品定价。我的报告分下面这几个部分，我会先介绍一下关联模型，但是考虑到我们这个会是应用型会议，所以我不会侧重在技术上面，而是在应用上面。紧接着我重点讲两个方面的应用，一是信用衍产品定价方面，就是CDO、BDS、CLO、CFXO等，第二部分是在二级资本债定价方面。

 

下面看一下为什么引入关联模型？它最重要的好处是可以刻画变量的联合分布，因为我们研究金融问题的时候需要做一些量化分析，需要获取变量间的相关性，尤其是对多元信用衍产品进行定价，还有投资组合分析的时候涉及变量间相关结构的分析，比如违约相关性，这个在资产证券化里面是一个很重要的问题。

 

对信用衍产品比较熟悉的人应该都知道David Li（李祥林），他有一篇文章，01年的时候发表在Journal of Fixed Income，也就是《固定收益证券》杂志，这篇文章讲的是用Copula模型做CDO的定价。他那个文章发表之后在华尔街广泛应用。但是在次贷危机之后对于这个模型有一些质疑，甚至影响了CDO的发行。之后的两年，大家有一些澄清。我们都知道模型是死的，人是活的，如果不灵活运用模型，都会出问题。所以我们不能对模型给予太多批评，而是如果模型有问题，我们可以改进。有这个作为基础，后面就好讲多了。

我下面要讲的工作是在李老师工作的基础上。09年年初的时候，关于李老师的工作有很多质疑，因为那个文章是用静态的关联模型进行定价，如果我们用动态的关联模型对信用衍生产品进行定价，我们可以克服这个弊端，所以这是我们做这个工作的原因。

 

那么我们刚才说了，在这之前都是线性相关系数刻画变量之间的相关性，但是它刻画的相关性不完全，有时甚至无法刻画。而Copula模型克服了线性相关系数的弊端，这是它当时出现的原因。有的朋友可能以前没有接触过关联模型，我简单说一下。我今天的演讲尽量少用模型，但是有模型大家理解得的更清楚，有必要的时候我会讲一些。

 

假设有两个变量，比如是两家公司的违约时间X和Y，我们知道它们的边缘分布，我们需要考察它们之间的违约相关性。从统计意义来说，我们就是要得到联合违约分布，也就是说，同时违约的概率多大。这个时候我们需要用联合概率来刻画，以往的研究都是假设二者服从联合正态。我们知道统计分析里面正态分布可以解决很多问题，而且它的一些指标很好算。但是我们现实生活中很多变量都是尖峰厚尾的，所以我们需要考虑如果不是正态我们怎么处理，关联模型可以解决这个问题。Copula这个单词是一个拉丁词，其实就是连系动词，就是一个桥梁，是边缘分布和联合分布之间的一个桥梁。我们国内统计学界的张尧庭老师，他给的一个翻译叫连接函数或关联函数。Copula有一个优势，它可以捕捉X和Y两个变量之间几乎所有的相关结构。比如说非对称、正向相关性、负向相关性、独立等，而且它可以构造很多种多元联合分布。我们在金融应用时经常需要寻找变量或者说股票回报之间的相关结构，在原有的研究中都是用多元正态分布刻画，但是正态分布不是一个好的刻画方法。

 

下面我给大家介绍五种常用的关联函数。一个是正态Copula，它的具体形式如下，有兴趣的可以找一些书来看。下面这个是学生t关联函数，紧接着是三个阿基米德关联函数。这三个Copula的好处是可以刻画非对称的相关结构。我们前几年做过一个研究，用97年东南亚金融危机的数据来研究，比如马来西亚的股市下跌的时候对于印尼股市是什么影响？这个问题从统计学上来看就是一个尾部相关性的问题，或者危机传染问题。次贷危机也是这样的，所以尾部相关性是金融里面的之一主要研究问题。这三种关联函数还有一个好处：我们可以看得出来，这个Copula函数里面只有一个参数阿尔法，所以我们做模拟的时候就非常简单。这三种Copula函数得第三个优点就是具体实现的时候比较简单。

下面我重点讲一下关联模型的应用。

 

下面是我们这几年的一些相关研究成果。第一篇，是用动态关联模型对篮子CDS进行定价，这个文章发表在《欧洲金融管理》杂志上。第二篇也是用关联函数对CDS进行定价，但是方法不一样，第三篇是对CDO进行定价，第四个是对CFXO进行定价。CDO里的D是债务，FX是外汇。所以都是对多元衍生产品进行定价。这是第一块。第二块儿是关于关联模型在二级资本债定价中的应用，这方面我们已经有四五篇成果。

下面我先介绍一下关于多元信用衍生产品的一个研究背景，然后重点以《欧洲金融管理》的这篇成果给大家汇报。我简要介绍一下这个模型和计算方法，最后用一个实例来做一个展示，最后我们会有数值计算的结果。

 

刚才讲到，静态关联模型是有问题的。我们知道，CDO一般是五年期，所以参考债务之间的关联结构不可能在五年内保持一成不变，这是一个很自然的直觉。所以我们需要研究动态的相关性，然后对篮子CDS（Basket CDS）进行定价，这是我们的研究背景。

大家可能对CDS很熟悉，因为我们去年9月，我国银行间交易商协会出了一个关于CDS的交易细则。其实我国在2010年的时候推出过中国版的CDS，也就是CRM，但推出之后交易量有限。去年9月份出来这个关于CDS的细则之后，在朋友圈流传一篇文章，里面关于CDS的描述有些误解。

 

下面说一下什么叫Basket  CDS。CDS是一个单一参考债务的信用衍生品，那么Basket  CDS是基于多个参考债务，是一揽子的贷款。一般的Basket CDS是基于3到6个参考债务。我们这篇文章里面假设有6个参考债务。这是CDS的一个结构图，大家可以看一下，我一般喜欢用欧债危机举例。当时希腊为了进入欧盟，让高盛设计了一款货币互换交易，但是设计这款互换之后，高盛其实知道希腊是没有能力进入欧盟的，因为它掩盖了一部分债务，所以担心希腊还不起钱。当时就跟德国一家银行买了基于希腊债务的CDS。所以当时高盛是信用保护买方，卖方是德国银行。如果希腊不违约的话，高盛定期支付德国银行一笔保险费。如果希腊还不起钱，作为信用保护卖方的德国银行支付一部分亏损给高盛。这是单标的的CDS，所谓多标的，就是说不仅仅是希腊，而是好几个国家的债务。如果有一家发生违约的时候信用保护卖方就进行赔偿，这样的BDS被称为首次违约互换，也就是First-to-defaultSwap，简称为FTD。然后是第二家违约的时候，也就是说有两家违约的时候信用保护卖方才需要支付，被称为Second-to-defaultSwap，简称为STD。一直到第三、第四、第五、第六，以此类推。所以它跟CDO有点像，也是一个分层的结构。

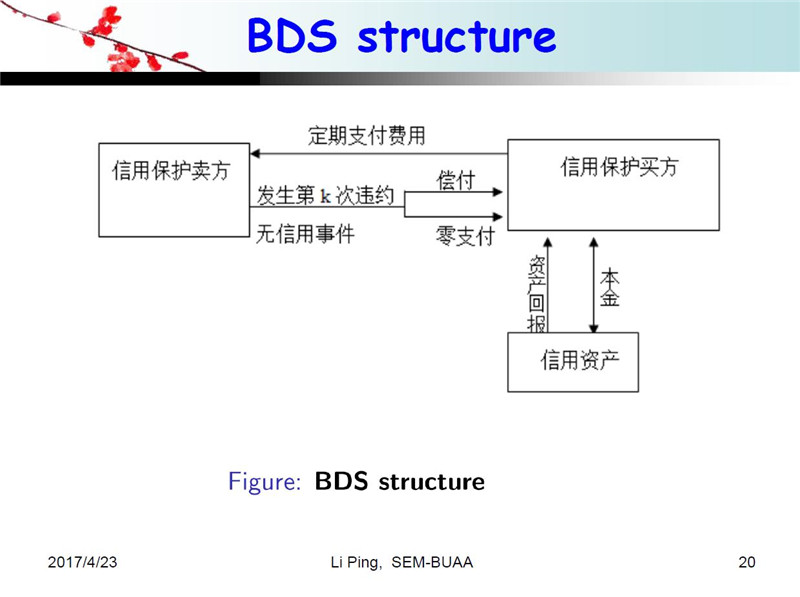
下面我介绍一下动态Copula模型。假设总共有六个债务，也就是六个变量，我们假设假设在时间S1的时候，关联函数发生了变化，比如说头一年可能是高斯关联函数，第二年可能是t关联函数。而第一年的头半年可能是参数为rho1的高斯关联函数，第二个半年可能是参数为rho2的高斯关联函数.所以我们精细地刻画了这个关联结构。

关于CDS定价，我们知道，一方面信用保护买方也就是高盛需要定期支付保费，这样我们算出所谓的payment leg；另一方面，如果发生违约，信用保护卖方也就是德国银行需要赔钱给信用保护买方，这样可以算出default leg，使得这两个leg相等的保费就是我们要计算的CDS的价格。这是CDS的定价思路，下面这个是我们的定价模型。

我们来看一下这个实例。我们选择了6个公司作为标的：中国联通、招行、武钢集团、中国石化、大众汽车和五矿发展，数据来自于yahoo金融。我们先估计6家公司的联合违约概率，这个太技术了，我就不详细讲了。我们考虑五个备选的关联函数，这里有一些统计方法比如AIC准则、二元分割法。根据我们的统计数据我们发现t关联函数是跟实际数据拟合得最好的。我们的数据期间是从2002年的10月9号到2012年4月27号，我们看十年期间六家公司的违约相关性的变化情况。我们最后根据关联结构的变化情况把十年数据划分成九段，每一段是不同的关联结构，有t关联函数，也有Frank关联函数，这是关联函数发生了变化，而且这几个变点都可以跟实际事件对上。这个结果我09年年底在哥伦比亚大学统计系讲过，他们很感兴趣，因为我们这个变点跟真实事件特别契合。比如我们可以找到股权分置改革，也就是05年的这个点，还有07年的5月份的印花税事件，以及次贷危机的影响等。这是我们的实际解释。

我们最后发现有一段时间关联函数没有发生变化，然后我们紧接着看关联函数的参数有没有发生变化。于是我们用统计方法发现，在其中一段虽然关联函数没有发生变化，但是参数发生了变化，这样我们把所有的参数变点也都找出来了。而且这些变点也跟实际事件相对应，包括非典、欧债危机等等。

 

找出关联结构只是第一步，我们的最终目的是对BDS进行定价。所以我们设计这样一个BDS，假设是07年4月份发行，然后5年的有效期，本金是一千万，我们假设它的本金一样，这样我们处理起来稍微简单一些。然后假设一个回收率，比如说70%，也就是说，发生危机时能回收70%，另外30%由信用保护卖方还。

下面这六个图是用我们的方法算出的BDS的价格，我们定价的时候不仅仅是对历史数据做，我们还要做样本外预测。刚才说六个标的，也就是说BDS有六层，所以我们对每一层进行了定价。为了验证我们这个模型的优点和性能，我们还和其他三种方法进行了比较，一个是静态高斯方法，紫色方块的线是静态高斯的定价结果，三角的线是静态t-Copula的结果，蓝色的线是动态高斯的结果，也就是说，Copula类型没有变化，但是参数发生了变化，黑色菱形的线是我们动态关联模型的定价结果，也就是说我们用四种模型对六层的结构进行了定价。

 

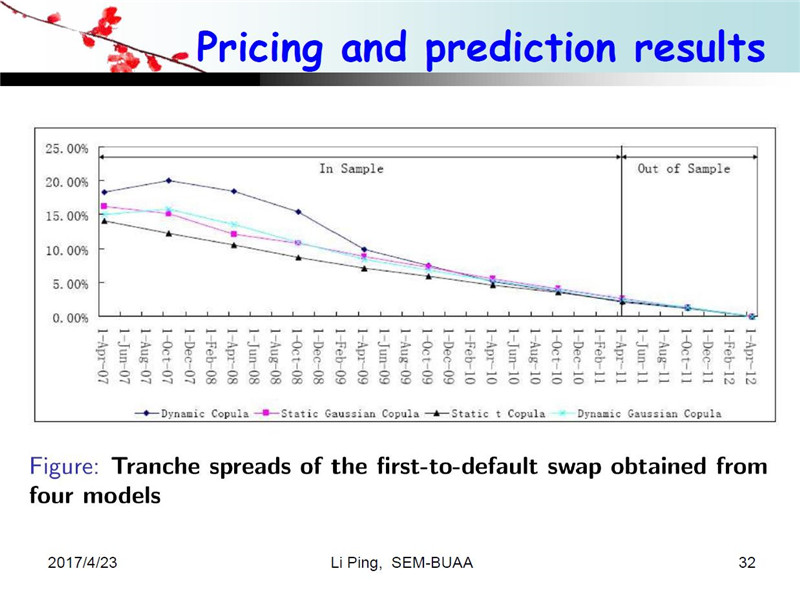
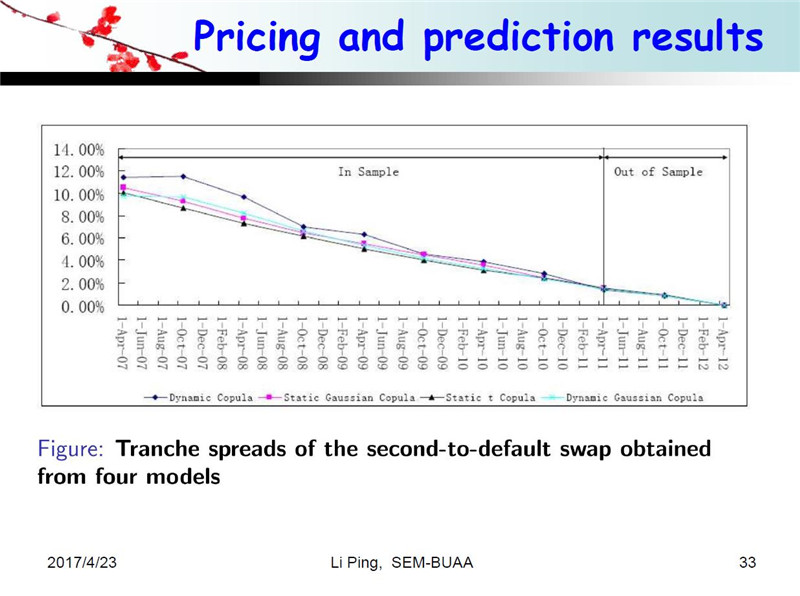
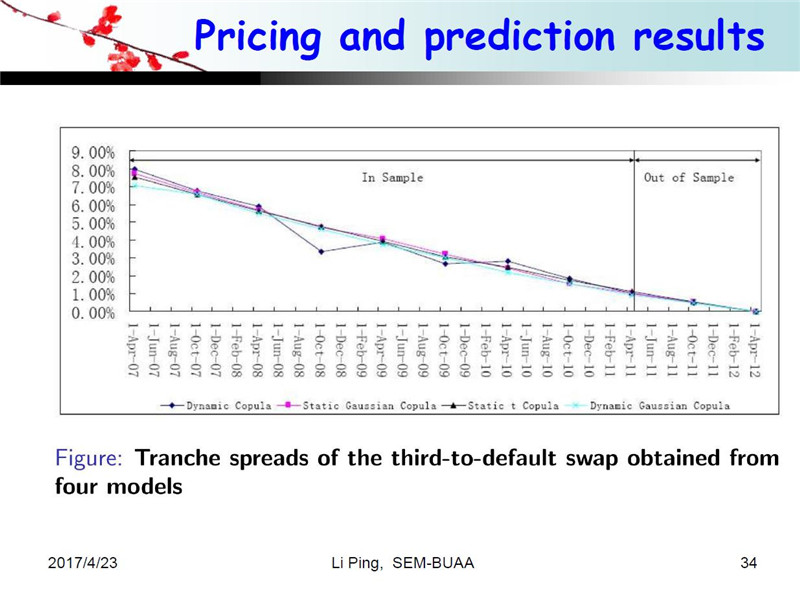
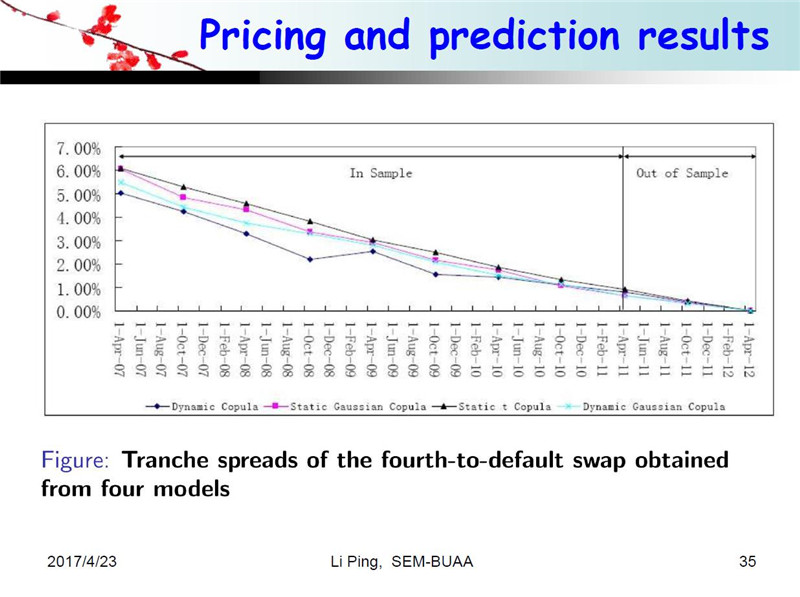
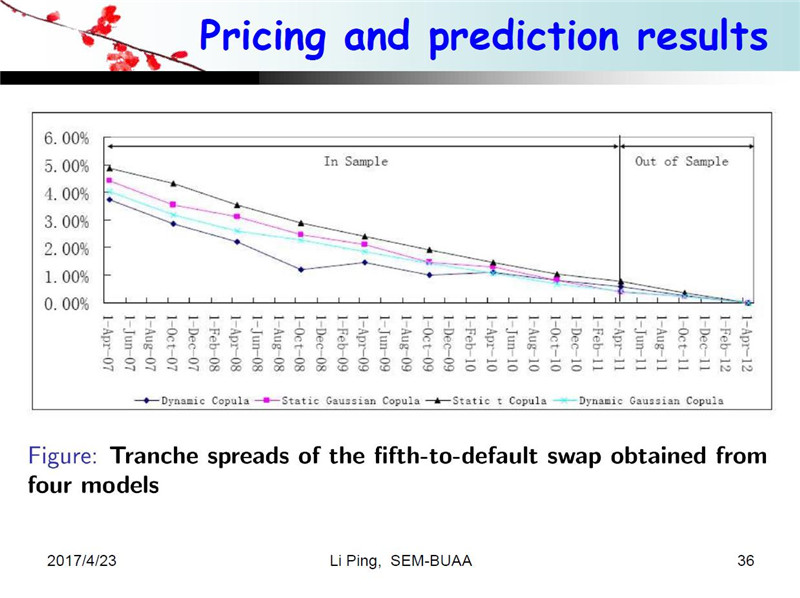
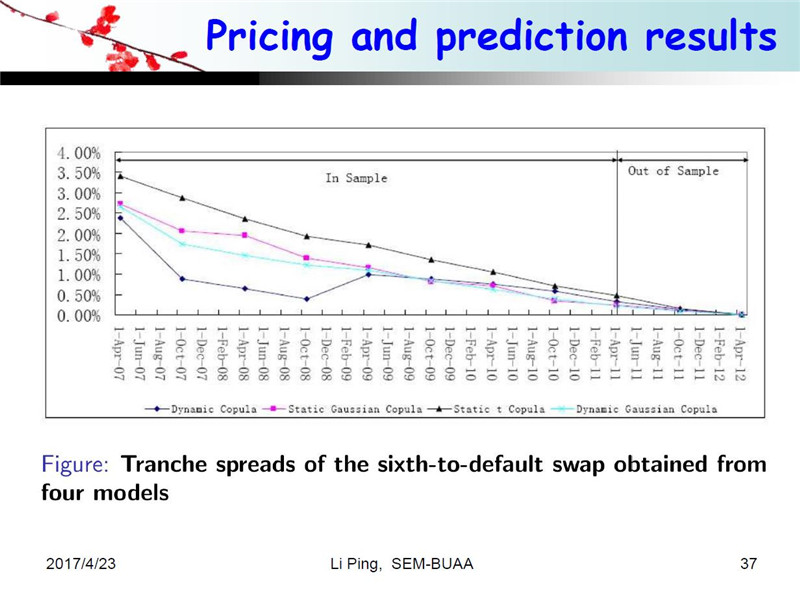
总共六个图，我给大家总结一下。先看第一层，结果非常明显，这是我们的数据，我们就会发现，对于第一层来说，我们的模型比这三个模型价格高一些，第一层第二层都是高一些的。而第五层和第六层我们的结果低一些。我们认为，因为我们考虑了动态相关结构而且是非高斯的情况，因此定价结果要比其他三种模型效果都要好一些。第三和第四层相对来说差距小一些，因为关联结构在这两层中的影响不是特别大。

上面是关于Basket  CDS的定价结果，下面我介绍一下我们在二级资本债方面的研究思路和结果。

 

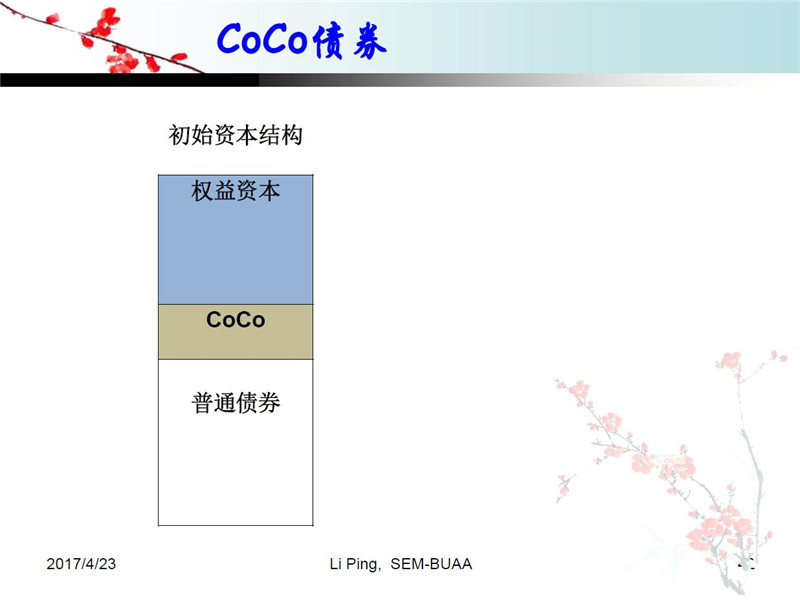
减记型二级资本债国际上叫CoCo债券，也有人叫可可债券。大家可以看一下这类债券的发行量，在国际上尤其是欧洲非常受欢迎，在美国有些争议。那到底什么叫CoCo债券呢？大家看这样一个图。这是一个公司或者银行的典型的资本结构，它包括权益资本、可可债券和普通债券。我们设计一个阈值，当有危机出现，导致股价和权益资本下降到到这个阈值时，可可债券释放出来转化为权益资本，补充资本金。这是它的大概结构。所以说，二级资本债是为了解决银行的资本充足率的问题。次贷危机之后我们知道有一个大而不能倒的问题，所以巴塞尔协议III在全球要求银行发行二级资本债，在危机的时候释放资金出来补充资本金。所以说它有债券和权益的双重属性，这样如果公司经营发生突发事件的时候根据一定比例发生减记，或者把债权转换成股权。

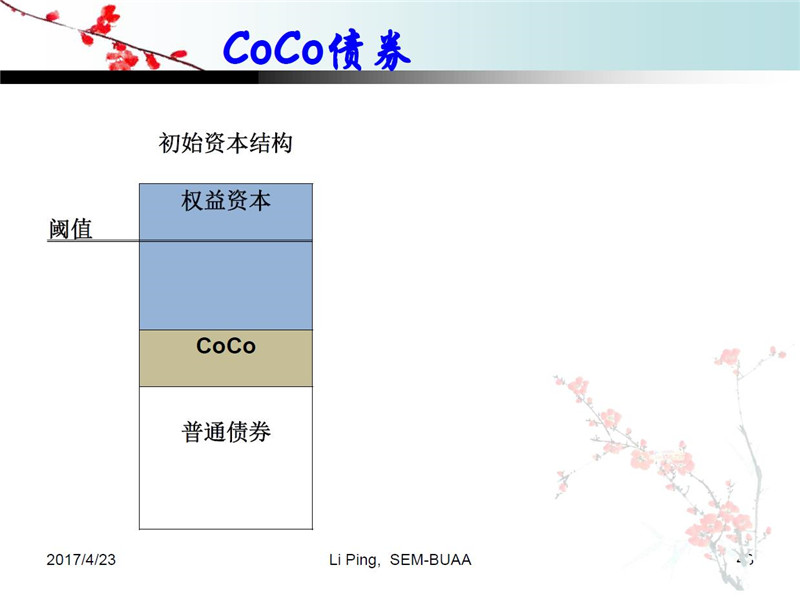
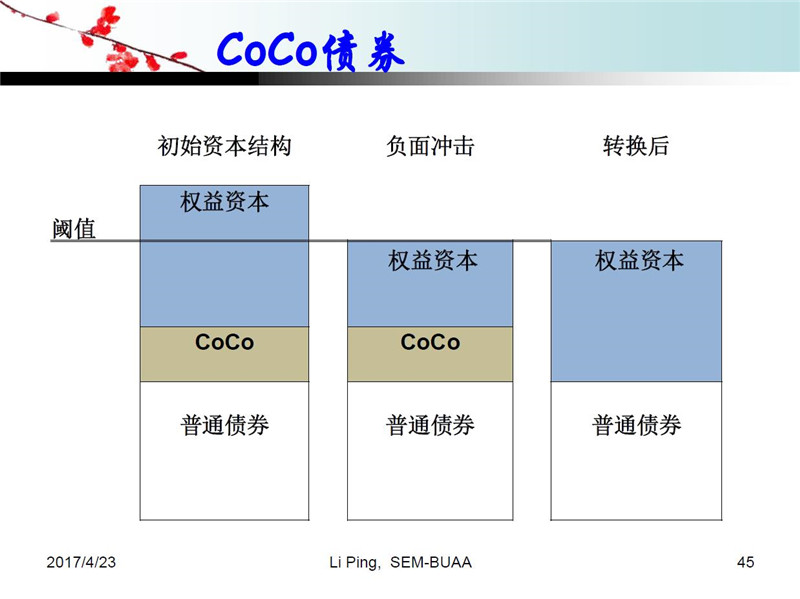
关于国内的发展情况，2012年我国证监会和银监会发布了指导意见，2013年滨海银行发行了第一款减记债，现在很多银行都有了，中国银行、农业银行这些大银行都有。

 

关于CoCo债券或减记债方面的研究状况，国际上之前的研究都是把核心一级资本比率CTR作为减记指标，但是没有考虑股价和核心一级资本比率的相关性。根据实际数据我们发现银行股价和CTR有相关性，所以我们用关联函数来刻画它们二者之间的相关结构，然后对二级资本债进行定价。我们用一些模型来刻画CTR和股价，然后对塞浦路斯银行发行的CECS这样一个CoCo债券做了一个实证债券，这是我们的主要结果。从这个图可以看出，用我们的模型做出来的定价结果比假设二者独立结果好很多。然后我们做了一个敏感性分析。最后我们结合国际上的CoCo债券和中国的监管实践，设计了适合中国国情的CoCo债券，并做了一个数值定价。

下面我总结和展望一下，我们国家的减记债以银监会的监管条例作为减记触发指标，根据我们的研究结果，我们认为应该把市场指标---比如股价---加进来作为减记触发指标，但是又不能完全看市场指标。

 

上面就是我关于关联模型在结构金融产品中的应用的介绍，谢谢大家。

 

李平简介：

北航经管学院金融系的教授、博导，中航重机独立董事，中国系统工程学会金融系统工程专业委员会的副秘书长。

教育经历：

中科院数学与系统科学研究院的博士、博士后。

海外经历：

先后在美国哥伦比亚大学、美国南卡罗莱纳大学、香港中文大学、香港城市大学、维也纳技术大学、德国洪堡大学等做访问学者。2015-2016年挂职首创集团金融管理部副总经理。